【分析編１】簡単で発見の多い分析：相関分析

「データ分析って難しそう。」

そうですね。
分析手法はたくさんあり、高度なものになると複雑な方程式やスキルが必要になります。

でも、簡単でかつ、発見の多い分析手法もあります。
今日はそれを紹介しましょう。

相関分析とは

相関分析とは異なる二つのデータの関係性を見るもので、以下のグラフのことを指します。

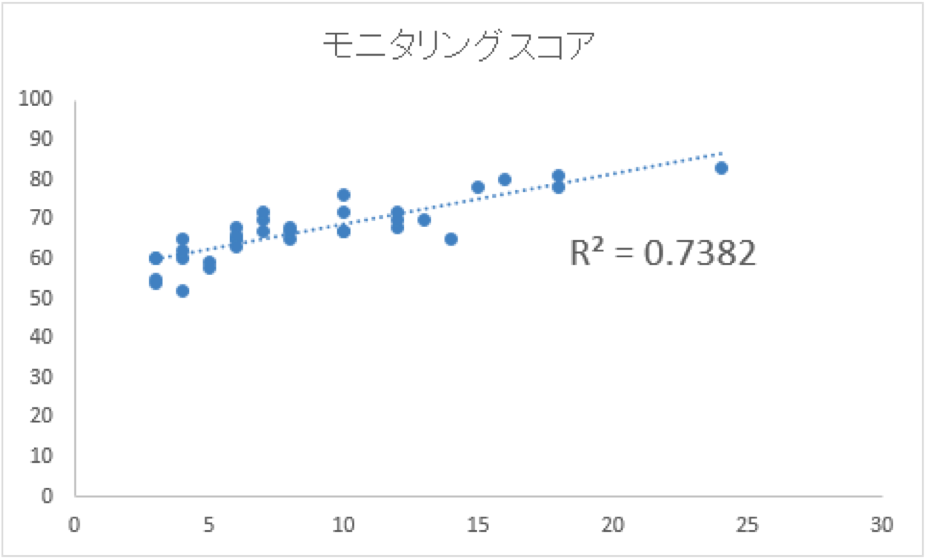
これは散布図のグラフを作るだけです。
簡単ですね。

皆さんはこんな疑問を感じていませんか。

● 在籍期間が長いほど、生産性は高いのかな？
● 電話応対スキルや生産性は、経験値に比例するのかな？
● 業務量が増えると、ミスも比例して増えるのだろうか？

これが本当かどうか、客観的に確認してみたくありませんか。
そんなときこそ、この相関分析が活躍してくれます。

興味がわいてきましたか。
それでは、どうやって作るかやってみましょう。

散布図の作り方

それでは、

「在籍期間が長いほど、電話応対におけるモニタリングスコアが高いのか？」

を例に散布図を作ってみましょう。

まず、オペレーターの在籍期間（月数）とモニタリングスコアの表を作ります。

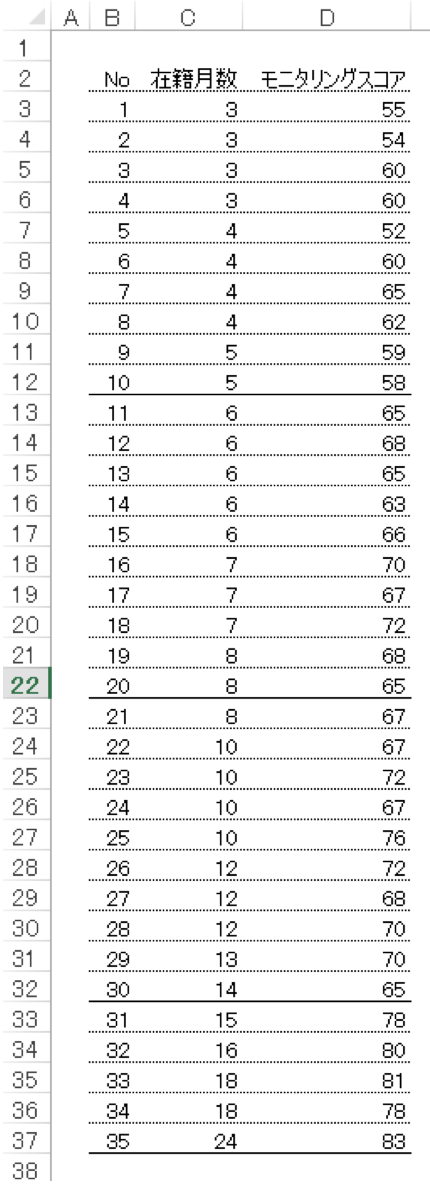
その表をカーソルで範囲を指定し、「挿入」タブをクリックして、グラフを選択します（ここまでの流れはグラフを作るのと同じ手順です。）

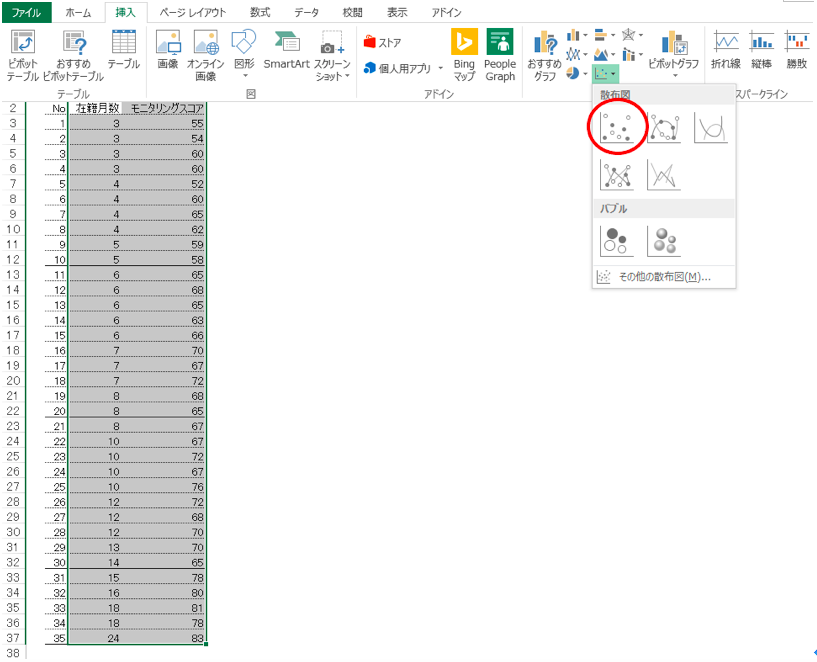
グラフは散布図の一番左上にある、点だけのものを選択します。

グラフが表示されました。

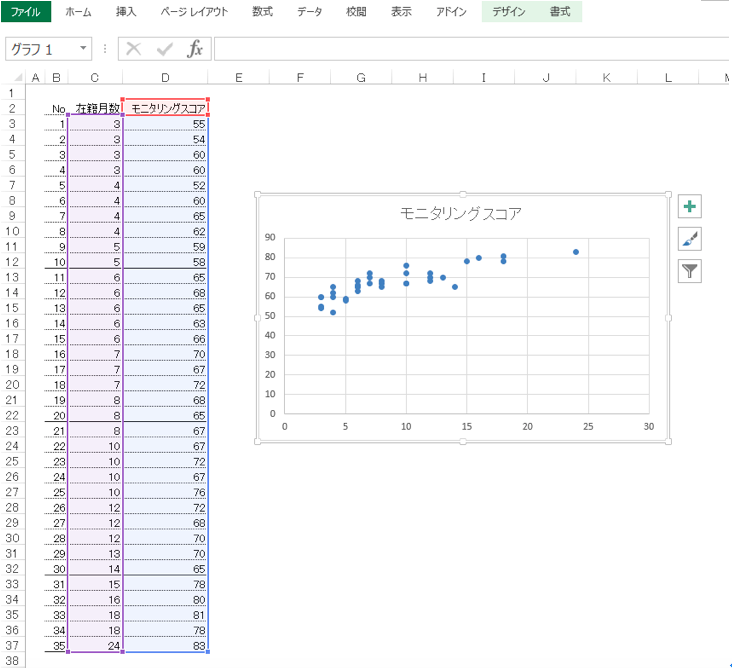
散布図は目盛線が邪魔になるので消します。
消し方は2通りあります。

通常方法

① グラフをクリックしてアクティブ状態にすると、メニューバーに「グラフツール」のタブメニューが表示されます。

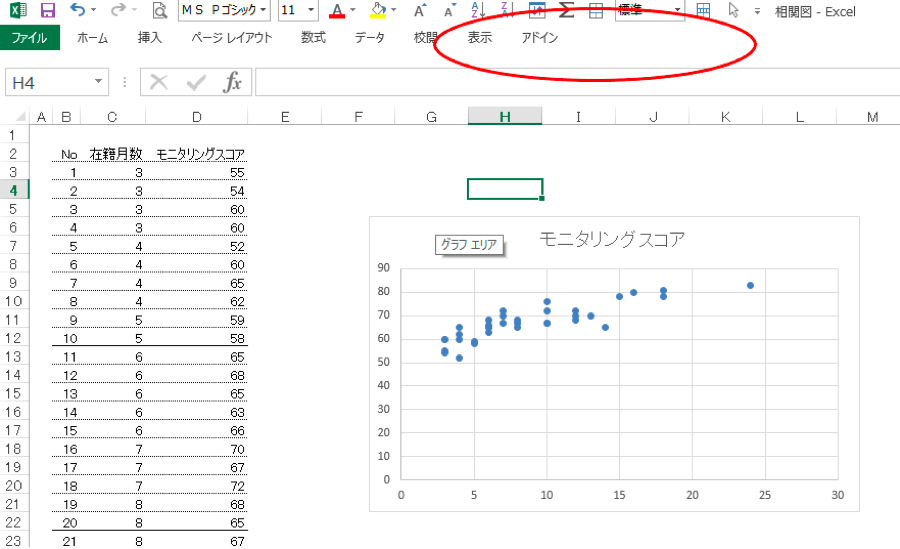
グラフ上のどこでもいいからクリックします。
⇩
上下の図でグラフの縁が変わりましたね。これが「グラフがアクティブ」になった状態です。

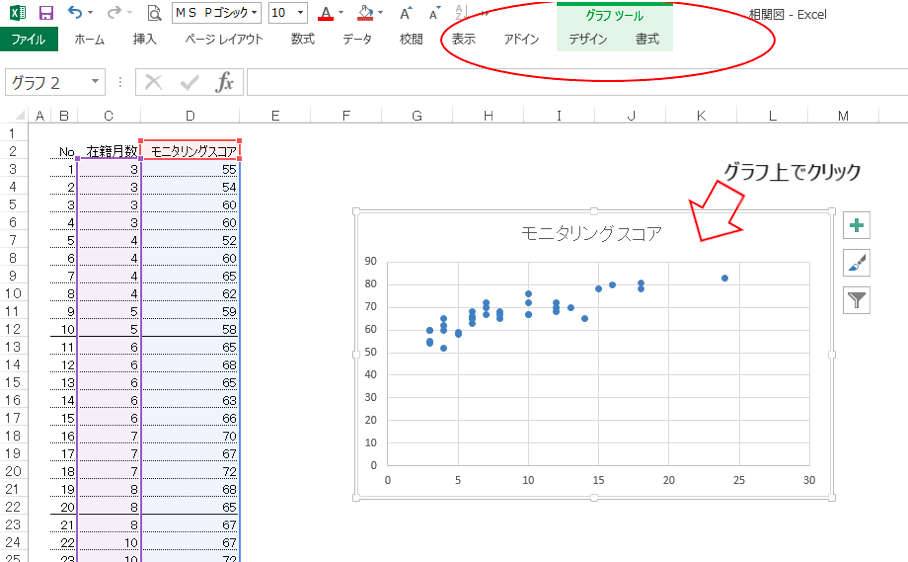
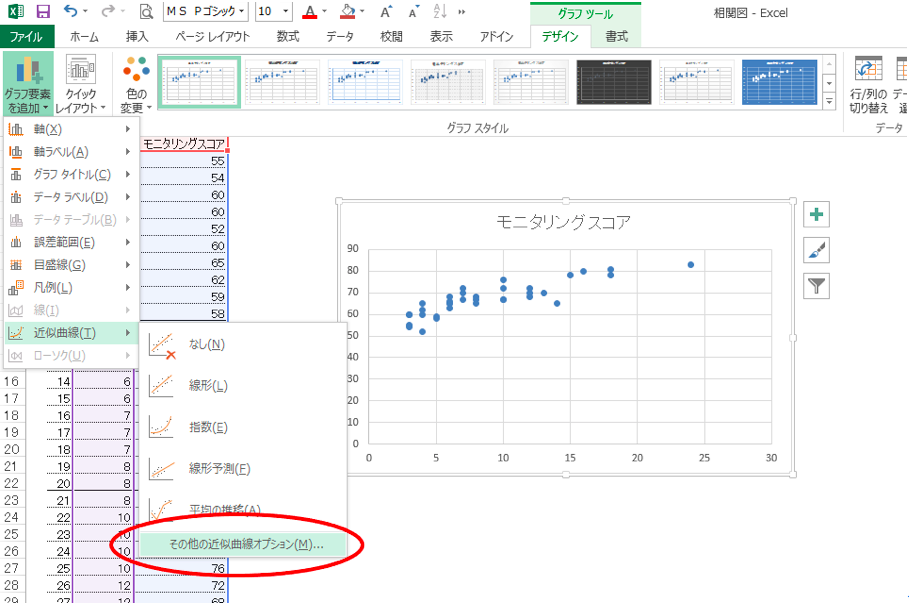
② デザインタブをクリック　→　一番左の「グラフ要素を追加」をクリック　→　「近似曲線」にカーソルを合わせる　→　「その他の近似曲線オプション」をクリック。

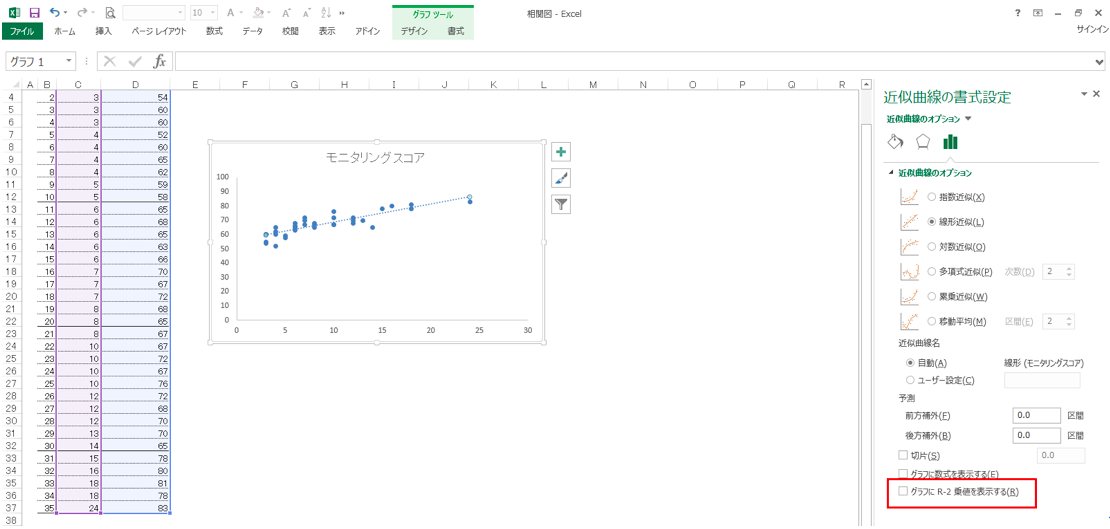
③ Excel右に「近似曲線の書式設定」が表示されたら、一番下にある「グラフにR=2乗値を表示する」にチェック。相関係数がグラフに表示される。

簡易方法

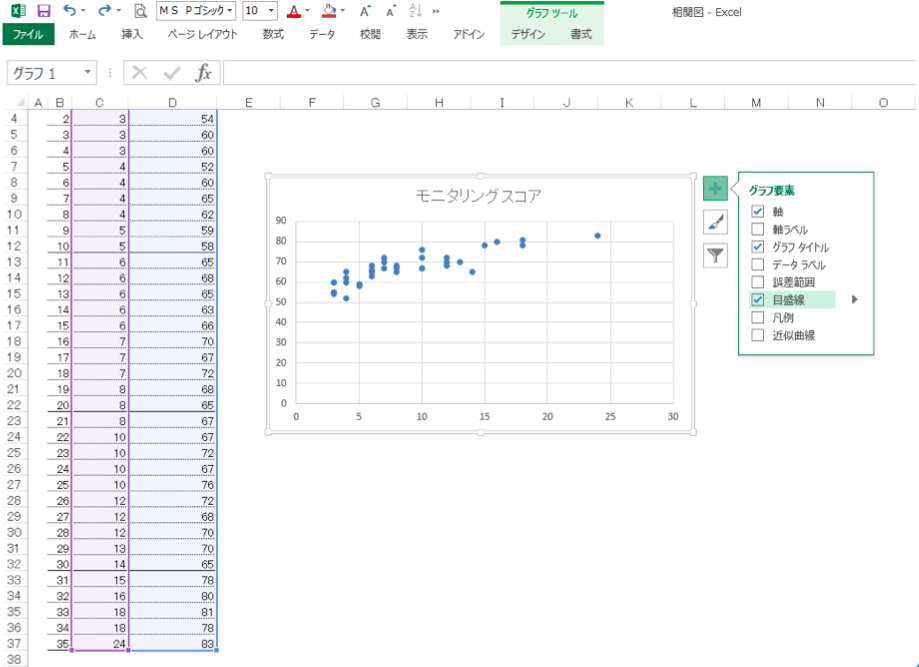
① グラフをクリックしてアクティブ状態にして、グラフ右上部に表示された「+」マークをクリック。

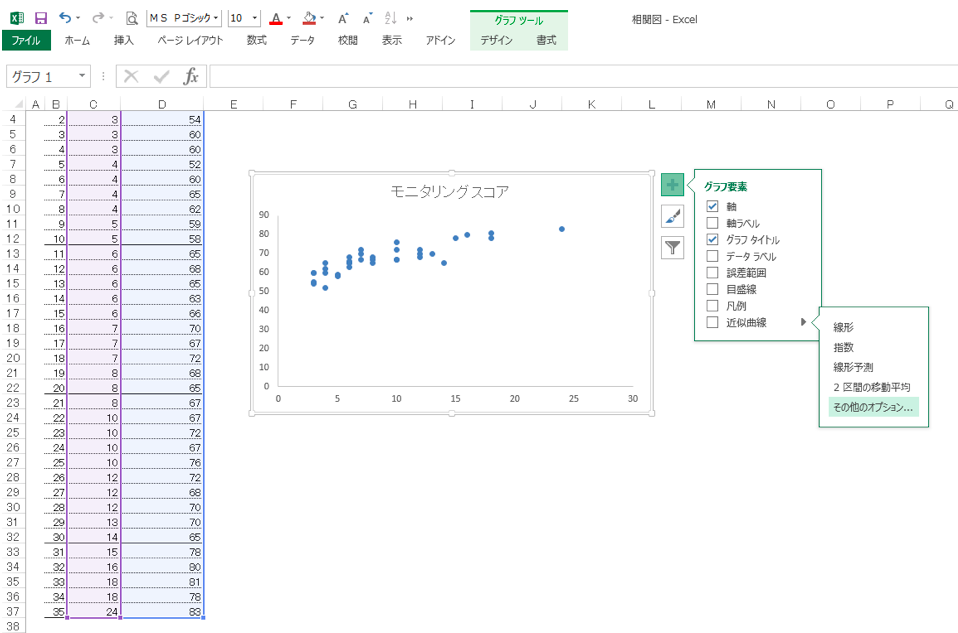
② 最下部の「近似曲線」にカーソルを合わせる　→　右に▶︎マークが表示されるのでクリック　→　「その他のオプション」をクリック。

③ Excel右に「近似曲線の書式設定」が表示されたら、一番下にある「グラフにR=2乗値を表示する」にチェック。相関係数がグラフに表示される。

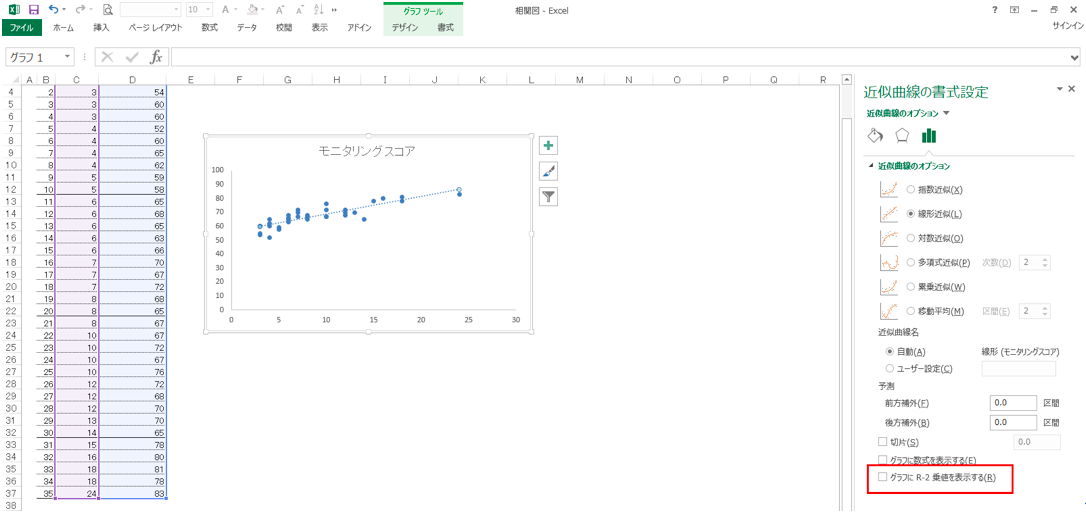
※「R-2乗値」とは

これは相関係数値で、範囲指定されたデータの相関度合いを0～1の範囲で表示します。数値は自動計算されます。
相関係数値が0に近いほど、二つのデータの相関が弱く、1に近いほど相関が強いとなります。

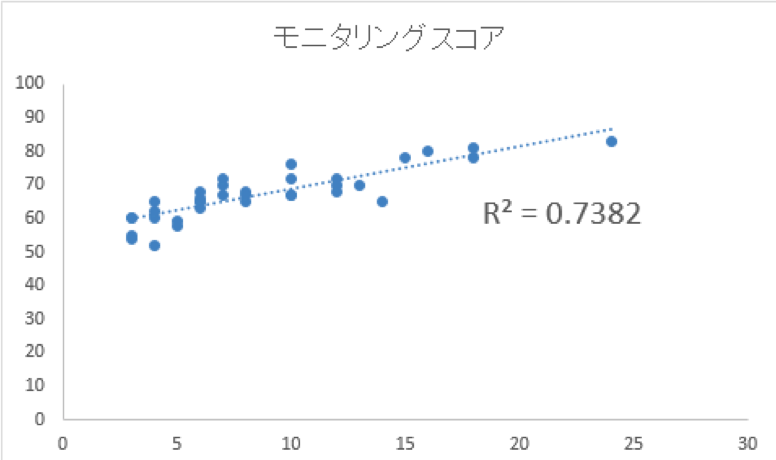
このグラフのケースでは相関係数値が0.7382と１により近いので、分析結果として在籍期間が長いほど応対スキルも高くなるという結論になります。

これが0.5以下であれば、在籍期間が長くとも応対スキルが向上するわけではないという結論を客観的に立証することができます。

どうですか？
折れ線グラフを作るようにグラフを作成したのち、ひと手間かけるだけです。
簡単ですね。

ただしひとつだけ注意点があります。
グラフを作成すると、異常値が出ることがあります。
例えば以下のケースです。

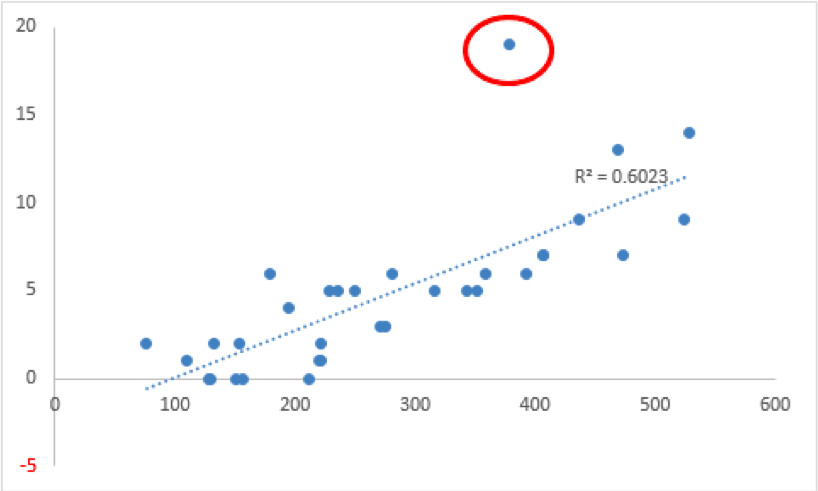
ひとつだけ極端に孤立した点（赤丸囲み）がありますね。
こういうデータが相関係数値に大きな影響を及ぼすので、こういうデータは除外する必要があります。

このデータを特定する方法は、その点の上にカーソルを合わせると、そのデータの値がカッコ内に表示されるので、表から該当するデータを探して消します。

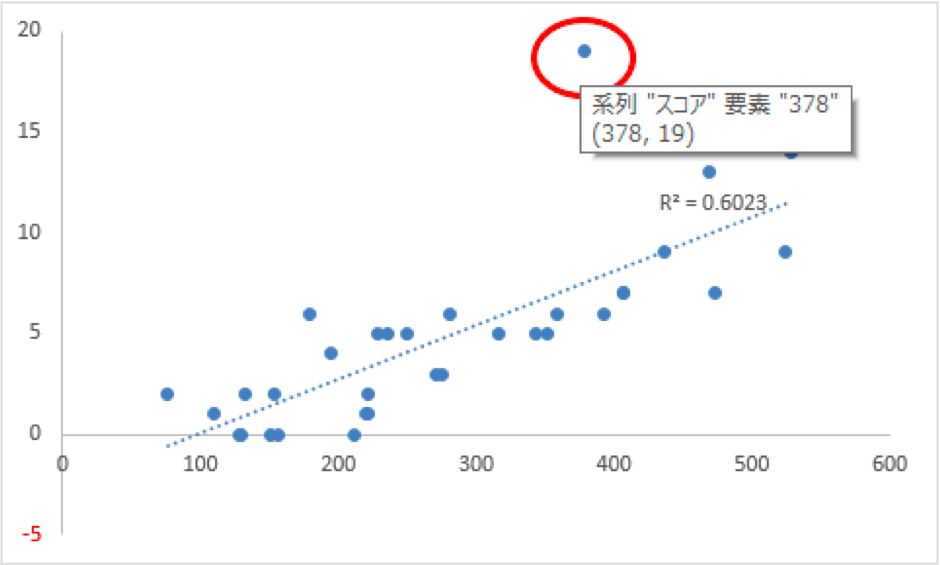
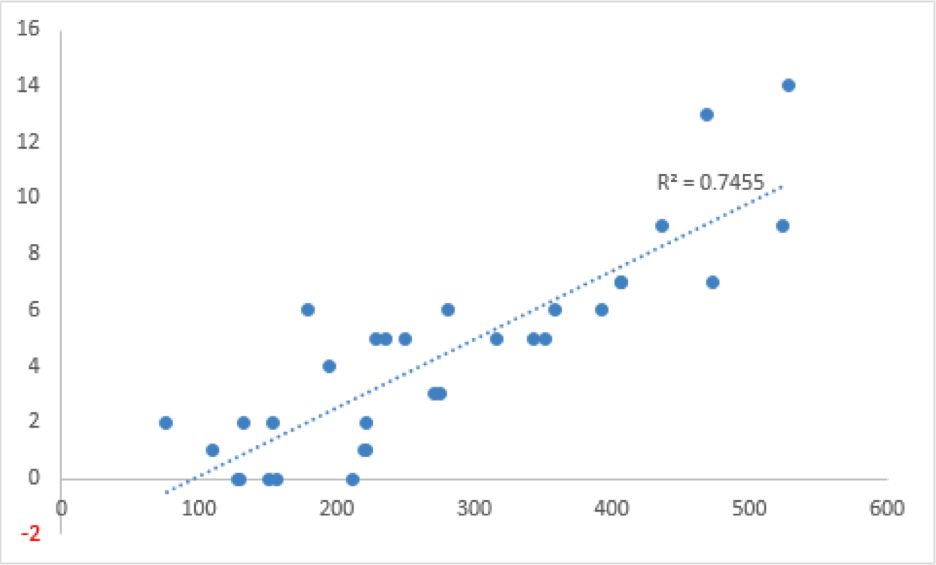
するとどうでしょう、相関係数値が0.6023→0.7455と変わりましたね。
今回のケースでは、「やや相関あり」から「強い相関あり」に変わりましたが、0.5前後の場合は全く異なる結論に変わる場合があるので、注意してください。

相関分析の活用例

この分析手法は様々な業界でも活用されています。

例えば、スーパーでは天気と来客数を相関分析したり、銀行では待ち時間の長さと取引件数との相関分析をしたりと、様々なケースで活用されています。

ひとつ相関分析を活用した事例を紹介します。

とあるコールセンターでは、コール数に対し必要人数を揃えているにもかかわらず、応答率が計画通りにならないことに悩んでいました。

このセンターでは比較的在籍期間の長いオペレーターが多くいました。したがって、業務デビュー後のフォロー教育はほとんど行われておらず、課題は業務の難易度の高さや新人のスキルが低すぎることにあるのではないかと、クライアントは考えていました。

そこで在籍期間に対し、通話時間、保留時間、後処理時間を相関分析してみました。
その結果が以下のグラフです。

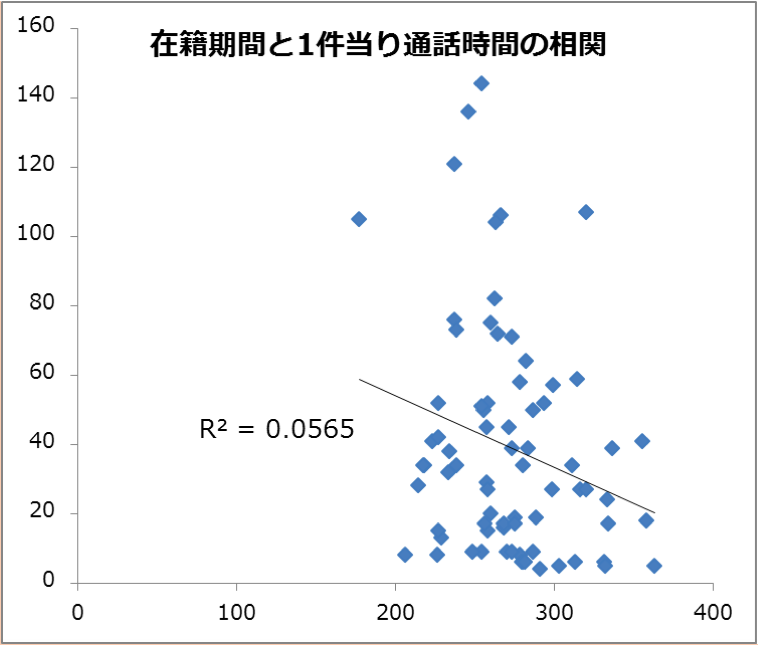
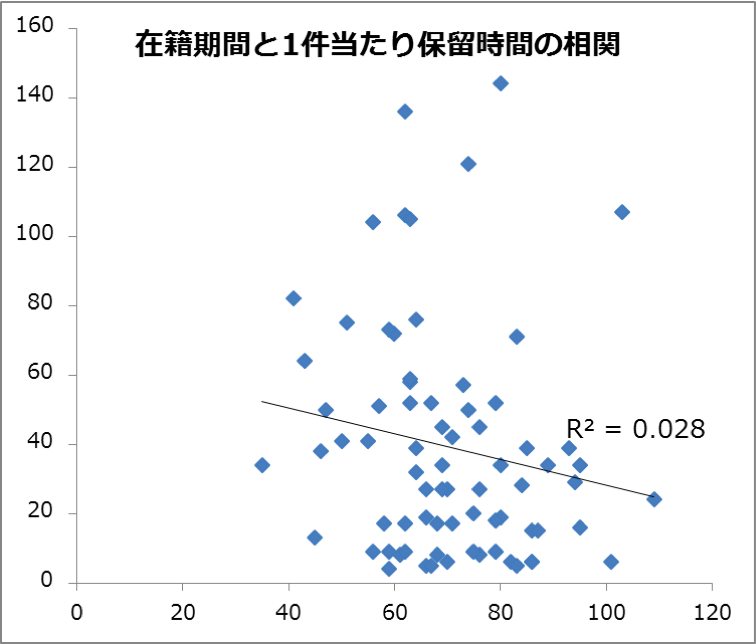
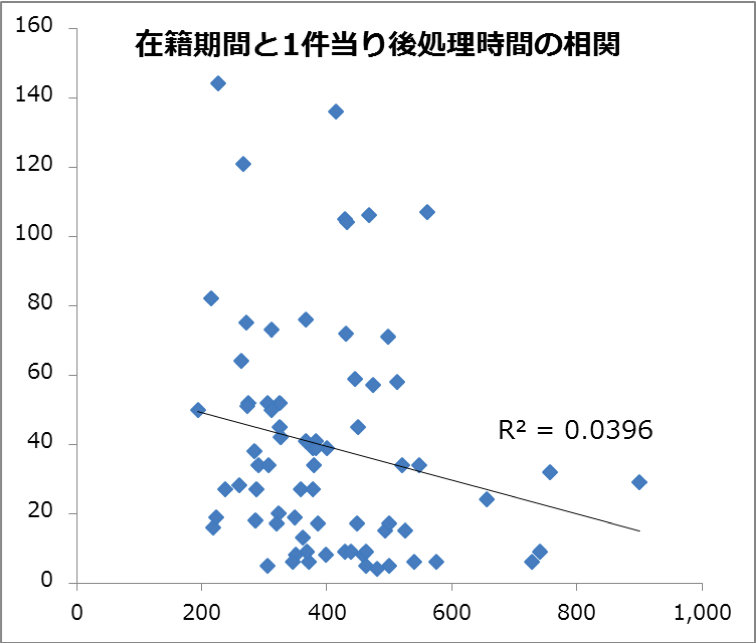
結果は、3つの処理時間全てにおいて限りなく0に近く、在籍期間と処理時間に全く相関が無いというものでした。

これは在籍期間が短くても処理時間が早い人は早く、逆に在籍期間が長くても処理時間が遅い人は遅いということを証明しています。

つまり「スキルは個に依存している」ということです。

ただちに組織的な生産性向上を目標とする教育を実施することになりました。

このケースに限らず、後処理時間と在籍期間の相関が無いと出るコールセンターは多く見受けられます。

このように何か課題を抱えている場合は、勘や経験に頼らず、客観的なアプローチをとることで、問題の本質をつかむことにつながります。

さあ、皆さんもさっそく分析してみましょう。何か見つかります！

次の記事はこちら

【分析編2】優先課題を絞り込む：パレート分析

＊【コールセンターのデータ分析　超入門】
分析を始める前に
グラフは見やすくかつ美しく!（前編・折れ線グラフの作り方）
グラフは見やすくかつ美しく!（後編・棒グラフの作り方）

＊【コールセンターのデータ分析　実践】
簡単で発見の多い分析：相関分析
優先課題を絞り込む：パレート分析
ピボットテーブルを使いこなして分析スピードアップ
ヒストグラムを使って改善ポイントの早期発見